Unveiling the Power of Visual Learning: Concept Maps in Mathematics
Related Articles: Unveiling the Power of Visual Learning: Concept Maps in Mathematics
Introduction
In this auspicious occasion, we are delighted to delve into the intriguing topic related to Unveiling the Power of Visual Learning: Concept Maps in Mathematics. Let’s weave interesting information and offer fresh perspectives to the readers.
Table of Content
Unveiling the Power of Visual Learning: Concept Maps in Mathematics
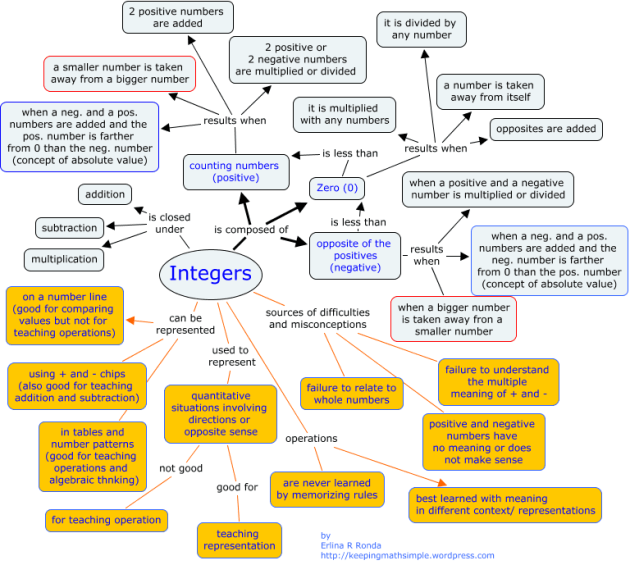
The realm of mathematics is often perceived as a complex tapestry woven with abstract ideas and intricate relationships. Navigating this landscape can be challenging, demanding a deep understanding of interconnected concepts. However, a powerful tool exists to illuminate this intricate web: the concept map.
Concept Mapping: A Visual Gateway to Mathematical Understanding
A concept map is a visual representation of knowledge, depicting relationships between ideas in a structured and hierarchical manner. It utilizes nodes, representing concepts, and connecting lines, signifying relationships between them. This visual framework transforms abstract mathematical ideas into tangible, easily digestible information.
The Mechanics of Concept Mapping in Mathematics
At its core, a concept map is a powerful tool for organizing and understanding mathematical concepts. It facilitates a clear and concise depiction of:
- Key Concepts: Each node in the map represents a fundamental concept, such as "number," "function," or "equation."
- Relationships: Connecting lines illustrate the relationship between these concepts, indicating hierarchies, dependencies, or connections. Labels on these lines clarify the nature of the relationship, such as "is a type of," "is defined by," or "is used to solve."
- Hierarchy: Concept maps often employ a hierarchical structure, with broader concepts at the top and more specific concepts branching out below. This visual hierarchy helps to clarify the interconnectedness of ideas.
Benefits of Concept Mapping in Mathematics
The benefits of utilizing concept maps in mathematics are multifaceted, enhancing learning and understanding across various levels:
1. Enhanced Comprehension and Retention: By visually organizing information, concept maps promote deeper understanding and retention. This visual representation allows students to grasp the interconnectedness of mathematical ideas, fostering a more holistic comprehension of the subject matter.
2. Improved Problem-Solving Skills: Concept maps can serve as a powerful tool for problem-solving. By identifying relevant concepts and their relationships, students can strategize effective solutions and navigate complex problems with greater clarity.
3. Active Learning and Engagement: The process of creating concept maps encourages active learning. Students actively engage with the material, identifying key concepts, analyzing relationships, and organizing information in a meaningful way.
4. Collaborative Learning and Communication: Concept maps facilitate collaborative learning and communication. By working together to create maps, students can share their understanding, challenge each other’s perspectives, and refine their understanding of mathematical concepts.
5. Assessment and Evaluation: Concept maps provide a valuable tool for assessment and evaluation. They offer a visual representation of a student’s understanding, revealing their grasp of concepts, their ability to identify relationships, and their overall understanding of the subject matter.
Constructing Effective Concept Maps in Mathematics
Creating effective concept maps requires a systematic approach:
1. Define the Topic: Clearly define the specific mathematical concept or topic you want to map. This provides focus and direction for your map.
2. Identify Key Concepts: Identify the key concepts related to the chosen topic. These are the fundamental building blocks of your map.
3. Establish Relationships: Analyze the relationships between these key concepts. Consider how they are interconnected, dependent, or related.
4. Visual Representation: Use nodes and connecting lines to visually represent the concepts and their relationships. Label these lines to clearly indicate the nature of the connection.
5. Hierarchical Structure: Organize the concepts in a hierarchical structure, placing broader concepts at the top and specific concepts branching out below.
6. Refinement and Iteration: Continuously refine and iterate your map as you learn more about the topic. Add new concepts, adjust relationships, and clarify connections to enhance the map’s effectiveness.
FAQs on Concept Maps in Mathematics
1. What are some common types of relationships used in concept maps in mathematics?
Common types of relationships include "is a type of," "is defined by," "is used to solve," "is a property of," "is an example of," and "is a consequence of."
2. Can concept maps be used for different levels of mathematics?
Yes, concept maps are applicable across all levels of mathematics, from elementary arithmetic to advanced calculus. The complexity of the map and the concepts included will vary depending on the level of study.
3. How can concept maps be used in classroom settings?
Concept maps can be used for a variety of purposes in classrooms, including:
- Pre-lesson review: Students can create maps to review prior knowledge before a new lesson.
- During-lesson exploration: Students can use concept maps to explore new concepts and identify relationships.
- Post-lesson consolidation: Students can create maps to summarize and consolidate their learning after a lesson.
- Assessment: Teachers can use concept maps to assess student understanding and identify areas for improvement.
4. Are there any software tools available for creating concept maps?
Yes, numerous software tools are available to assist in creating concept maps. Some popular options include:
- Coggle: A collaborative online tool for creating and sharing concept maps.
- Mindomo: A versatile mind mapping and concept mapping tool with a user-friendly interface.
- XMind: A powerful mind mapping tool that also offers features for creating concept maps.
Tips for Utilizing Concept Maps in Mathematics
1. Start Small: Begin with simple concept maps focusing on a single concept or a small group of related ideas. As you gain confidence, you can gradually expand the complexity of your maps.
2. Be Clear and Concise: Use clear and concise language to label nodes and connecting lines. Avoid jargon or overly complex terminology.
3. Use Visual Cues: Utilize different colors, shapes, or sizes to differentiate concepts and relationships. This visual distinction can enhance clarity and understanding.
4. Seek Feedback: Share your concept maps with others and seek feedback. This can help you identify areas for improvement and refine your understanding.
5. Practice Regularly: Regularly creating and using concept maps will enhance your ability to visualize and understand mathematical relationships.
Conclusion: Concept Maps – A Powerful Tool for Mathematical Exploration
Concept mapping provides a powerful visual framework for navigating the intricate landscape of mathematics. By organizing concepts, identifying relationships, and promoting active learning, concept maps enhance understanding, foster problem-solving skills, and create a more engaging and effective learning experience. As you embark on your mathematical journey, consider the power of visual representation through concept maps. They can unlock new insights, deepen your understanding, and illuminate the interconnected beauty of mathematical ideas.

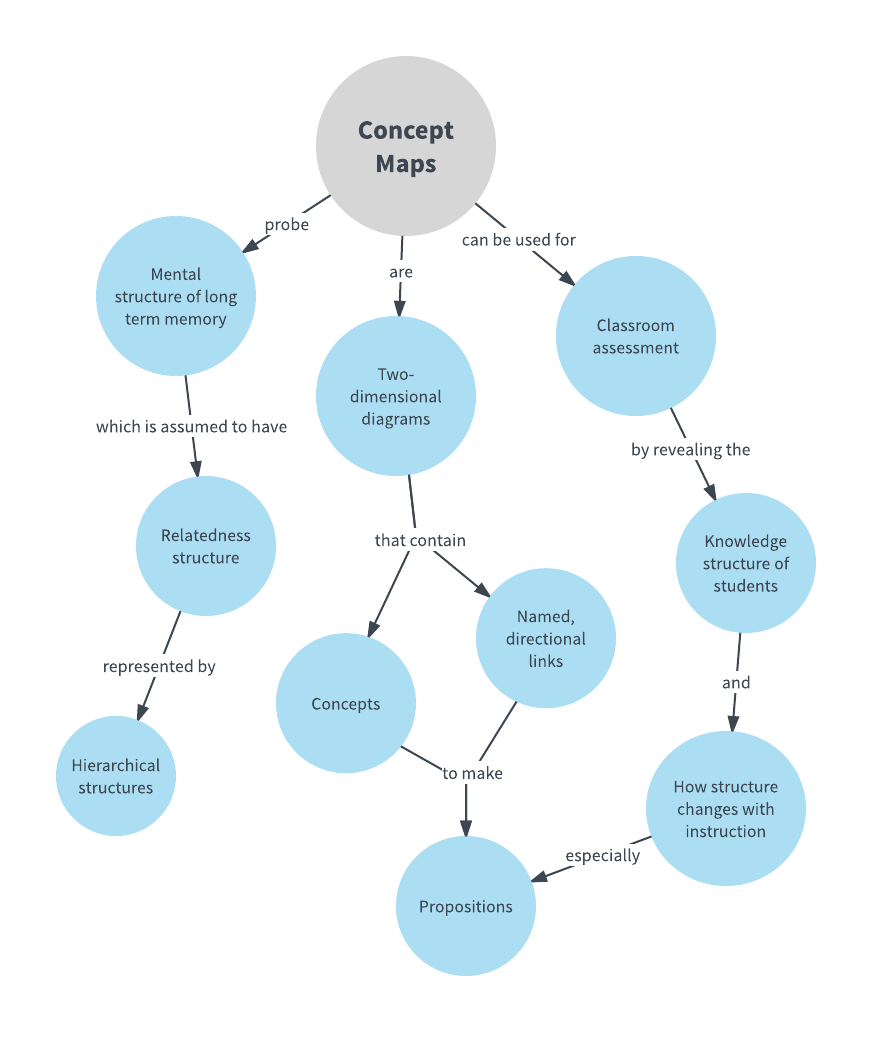




Closure
Thus, we hope this article has provided valuable insights into Unveiling the Power of Visual Learning: Concept Maps in Mathematics. We thank you for taking the time to read this article. See you in our next article!